1. 線形と非線形の本質的な違い
フィッティングにおける「線形」「非線形」の区別は、関数の見た目(グラフが直線か曲線か)ではなく、モデル式が未知パラメータに対して線形であるかによって決まります。
- 線形モデル: \(y = ax + b\) や \(y = ax^2 + bx + c\) など。\(x^2\) の項があっても、未知パラメータ \(a, b, c\) に対しては線形(1次)です。最適解は数学的に一意に求まります。
- 非線形モデル: \(y = A \cdot \exp(-kt)\) など。パラメータ \(k\) が指数などに含まれており、パラメータに対して線形ではありません。
非線形モデルでは、最適解を直接計算(解析的に解く)することができません。そのため、コンピュータを用いた反復計算によって、最適解を探索する必要があります。
2. 最小二乗法
非線形フィッティングの核心は、「いかにして効率的に最適解にたどり着くか」という探索アルゴリズムにあります。すべてのデータ点 \((x_i, y_i)\) とモデル関数 \(f(x_i, \boldsymbol{p})\) との残差(誤差)の平方和 \(S\) を最小化するパラメータ \(\boldsymbol{p}\) を見つけるのがゴールです。
$$ S(\boldsymbol{p}) = \sum_{i=1}^{n} (y_i – f(x_i, \boldsymbol{p}))^2 $$
\(S\) はパラメータ空間上の超曲面を形成します。この曲面の最も低い「谷底」を探すのが、これから紹介するアルゴリズムの役割です。
3 主なアルゴリズム
ガウス・ニュートン法 (Gauss-Newton Method)
線形近似に基づいた最も基本的な手法です。各ステップで残差平方和 \(S\) を最小化するような次のパラメータ更新量を、正規方程式を解くことで直接計算します。最適解の近傍では収束が速い(二次収束)という利点がありますが、初期値が解から遠い場合や、モデルの曲率が大きい場合に不安定になり、発散してしまうことがあります。
レーベンバーグ・マーカート法 (Levenberg-Marquardt Method)
現在、非線形フィッティングで標準的に用いられる非常に強力なアルゴリズムです。ガウス・ニュートン法に、最急降下法の要素を組み合わせることで安定性を高めています。
以下で説明するpythonのライブラリは、レーベンバーグ・マーカート法を用いています。説明は簡単ですが、内部構造の構築はとても困難です。。。
4. Pythonによる具体的な実装例
理論は複雑ですが、現代ではライブラリを使えば誰でも簡単に非線形フィッティングを実行できます。ここでは、Pythonと、そのライブラリであるSciPyを使った実装方法を紹介します。以下のサンプルデータを使って説明します。
このデータは、指数関数的減少をする実験データサンプルです。pythonコードと同じフォルダに入れましょう。
サンプルcsvファイル4.1 準備:ライブラリのインポート
まず、データ操作のためのPandas、数値計算のためのNumPy、グラフ描画のためのMatplotlib、そしてフィッティングを実行するためのSciPyからcurve_fit関数をインポートします。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
import japanize_matplotlib # 日本語で図のタイトルを入れられるようにする
4.2 データの読み込みと準備
次に、Pandasライブラリのread_csv関数を使って、ダウンロードしたデータファイルを読み込みます。ファイルが正しく読み込めたら、解析に使う列(’Time’と’Value’)を抽出して、それぞれをNumPy配列として準備します。
# CSVファイルを読み込む
try:
df = pd.read_csv('experimental_data.csv')
print("CSVファイルの読み込みに成功しました。")
except FileNotFoundError:
print("エラー: 'experimental_data.csv'が見つかりません。")
print("スクリプトと同じフォルダにファイルを保存してください。")
exit() # ファイルが見つからない場合は終了
# DataFrameからxデータとyデータを抽出
t_data = df['Time'].values
y_data = df['Value'].values
4.3 モデル関数の定義
読み込んだデータにあてはめたい数式モデルをPythonの関数として定義します。
# フィッティングするモデル関数(指数関数的減衰)
def exponential_decay(t, A, k):
return A * np.exp(-k * t)
4.4 フィッティングの実行と結果の可視化
準備が整ったら、curve_fit関数にモデル関数と読み込んだデータを渡してフィッティングを実行します。得られた最適パラメータを使って、元のデータとフィット曲線を重ねてプロットし、結果を視覚的に確認します。
# --- フィッティングの実行 ---
popt, pcov = curve_fit(exponential_decay, t_data, y_data)
# --- 結果の表示 ---
A_fit, k_fit = popt
print(f"最適化されたパラメータ: A = {A_fit:.3f}, k = {k_fit:.3f}")
# --- グラフ描画 ---
plt.figure(figsize=(10, 6))
plt.scatter(t_data, y_data, label='実験データ (from CSV)', color='royalblue')
t_fit = np.linspace(t_data.min(), t_data.max(), 200)
plt.plot(t_fit, exponential_decay(t_fit, A_fit, k_fit), 'r-', label='フィッティング曲線')
plt.title('非線形フィッティングの結果')
plt.xlabel('時間 (t)')
plt.ylabel('測定値 (y)')
plt.legend()
plt.grid(True)
plt.show()
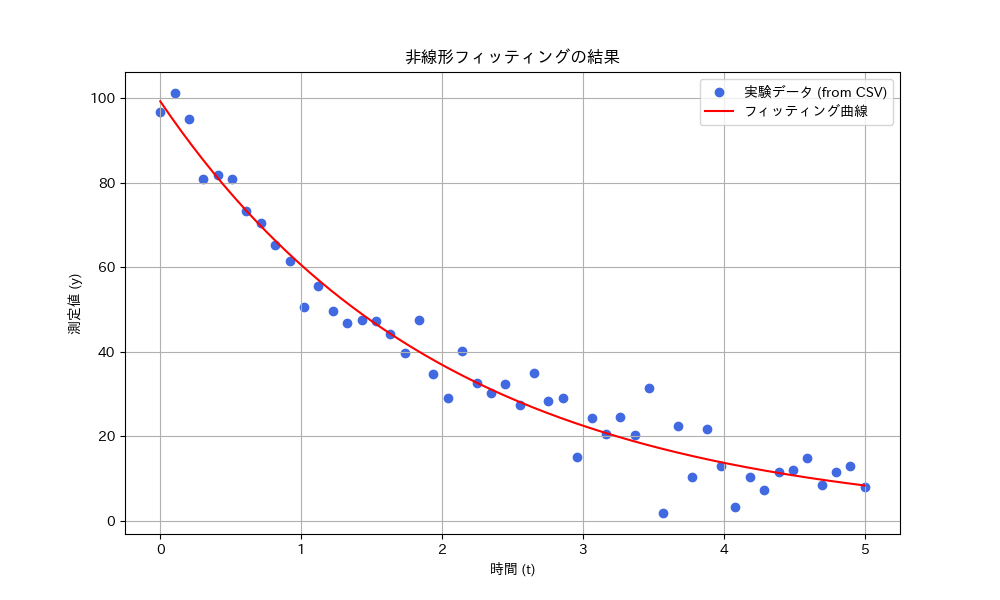
4.5 こんな感じの結果が出るはず
以下のような結果がでたら成功です。指数関数の”ように”減少していたデータに対して最小自乗法を用いて曲線を引くことができました。
5.フィットの良さを示す指標:決定係数 (R²)
最適化された関数が、元のデータにどれくらいうまく当てはまっているかを知りたいですよね。そのフィットの良さを示す最も代表的な指標が「決定係数 (R²)」です。
決定係数は、モデルがデータの「ばらつき」をどれだけうまく説明できているかを示す指標で、0から1の間の値をとります。1に近いほど、当てはまりが良い(=説明できている)と評価できます。
5.1 決定係数の考え方
少し例えてみましょう。データの「ばらつき」の合計量を100点のテストだと考えてみてください。
- R² = 0.95 の場合: 「あなたのモデルは、テスト範囲(データの全ばらつき)のうち95点分を説明できました!」という意味です。
- R² = 0.50 の場合: 「モデルは、テスト範囲の半分、50点分しか説明できていません。改善の余地がありそうです」という意味です。
このように、R²は「データ全体のばらつきのうち、作成したモデルで説明できた割合」と解釈すると分かりやすいです。
5.2 計算式とPythonコード
決定係数は、以下の式で計算されます。
$$R^2 = 1 – \frac{\sum_i (y_i – f_i)^2}{\sum_i (y_i – \bar{y})^2}$$
ここで、分子は「モデルで説明できなかったズレ(残差)の合計」、分母は「データ全体のばらつきの合計」を表しています。Pythonでは、フィッティングで得られた最適パラメータpoptを使って以下のように計算できます。
# poptはフィッティングで得られた最適パラメータ
# y_dataは実測データ
# 残差(実測値 - 予測値)を計算
residuals = y_data - exponential_decay(t_data, *popt)
# 残差の平方和 (モデルで説明できなかった部分) を計算
ss_res = np.sum(residuals**2)
# 全体のばらつき(実測値 - 平均値)の平方和を計算
ss_tot = np.sum((y_data - np.mean(y_data))**2)
# 決定係数を計算
r_squared = 1 - (ss_res / ss_tot)
print(f"決定係数 (R^2): {r_squared:.4f}")
5.3 利用上の注意点
決定係数は非常に便利な指標ですが、万能ではありません。例えば、不必要に複雑なモデル(過学習)を使うと、R²は簡単に1に近づいてしまいます。そのため、R²の値だけで判断せず、必ずグラフや残差プロットと合わせて総合的にフィットの良し悪しを評価することが重要です。
5.フィッティングパラメータの不確かさ
フィッティングによって得られたパラメータは、あくまで最も「それらしい」値であり、真の値そのものではありません。では、その最適値がどのくらい信頼できるのでしょうか?その信頼性の度合いを示すのが「不確かさ (uncertainty)」、あるいは標準誤差 (standard error) と呼ばれる指標です。
幸いなことに、この不確かさは、フィッティングの副産物である共分散行列 (pcov) から簡単に計算することができます。
# pcovの対角成分から分散を取得し、その平方根を計算して標準誤差を求める
perr = np.sqrt(np.diag(pcov))
# 結果の表示
A_fit, k_fit = popt
A_err, k_err = perr
print("--- フィッティング結果 (不確かさを含む) ---")
print(f"A = {A_fit:.3f} ± {A_err:.3f}")
print(f"k = {k_fit:.3f} ± {k_err:.3f}")
実験結果は、不確かさと一緒に記すことで大きな意味を持ちます。不確かさの計算を忘れないようにしましょう。
