近似直線

1.近似直線

1.1近似直線(回帰直線)とは

物理現象が理論的に一次関数になる。このような状況で理論と実験を照らし合わせるための手法である。例えば、フックの法則がそれにあたる。

\[F=kx\]

実験で、力\(F\)とばねの伸び\(x\)を計測したとして、以下の結果が得られた場合を考える。

ばねの力と変位の実験データ

変位 \(x\) [m]	力 \(F\) [N]
0.00	0.03
0.10	0.30
0.20	0.59
0.30	0.94
0.40	1.17
0.50	1.50
0.60	1.85
0.70	2.08
0.80	2.41
0.90	2.68
1.00	3.02

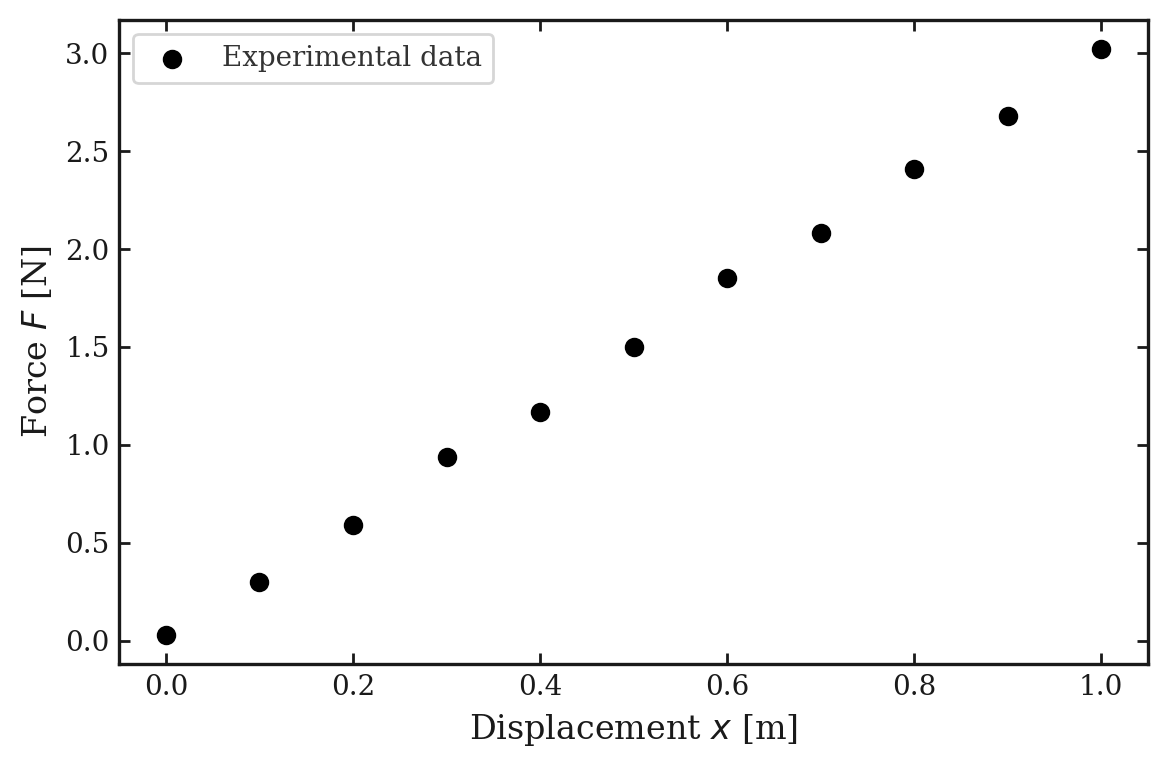
ここにふさわしい直線を計算することができ、今回の場合は

\[ F = (2.99 \pm 0.03)\,x + (0.011 \pm 0.015) \]

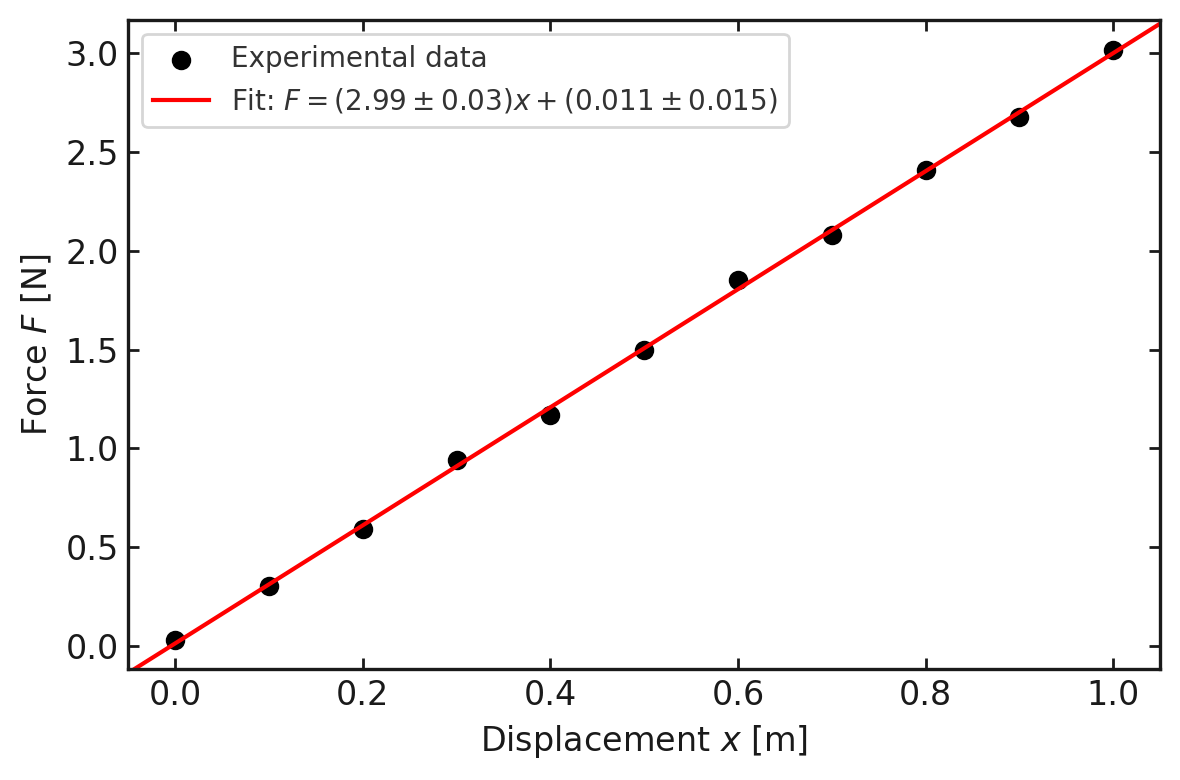
となる。次の章で具体的な計算方法を見る。

1.2近似直線の計算法(最小二乗法)

次のような状況を考える。

理論的に一次関数になる N 個の実験データ

\(Y\) [unit]	\(X\) [unit2]
y1	x1
y2	x2
⋮	⋮
yk	xk
⋮	⋮
yN	xN

次を計算しておく。

\[S_X=\sum_{k=1}^{N}x_k,\quad S_Y=\sum_{k=1}^{N}y_k ,\quad S_{X^2}=\sum_{k=1}^{N}x_k^2 ,\quad S_{Y^2}=\sum_{k=1}^{N}y_k^2 ,\quad S_{XY}=\sum_{k=1}^{N}x_ky_k\]

このような実験結果が、どんな一次関数できるかは、次の式でもとまる。傾きと切片は

\[a=\frac{NS_{XY}-S_XS_Y}{NS_{X^2}-S_X^2},\quad b=\frac{S_{X^2}S_{Y}-S_XS_{XY}}{NS_{X^2}-S_X^2}\]

で計算できる。しかし、これではこのデータの信用度がわからない。不確かさを計算する必要がある。\(S_X^2\neq S_{X^2}\)に注意。

1.3近似直線の不確かさ

不確かさは、次の式で求められる。実際に具体例で計算すると身につくかもしれない。

\[\sigma_{\bar{a}}=\sigma_{\bar{Y}}\sqrt{\frac{N}{NS_{X^2}-S_X^2}},\quad \sigma_{\bar{b}}=\sigma_{\bar{Y}}\sqrt{\frac{S_{X^2}}{NS_{X^2}-S_X^2}}\] \[\text{ただし}~~~\sigma_{\bar{Y}}=\sqrt{\frac{1}{N-2}\sum_{k=1}^{N}\left(y_k-ax_k-b \right)^2 }\]

まとめて、次のように表記する。有効数字は、不確かさの慣例に従う。

\[Y=\left(a\pm \sigma_{\bar{a}}\right)X+\left(b\pm \sigma_{\bar{b}}\right) \]

2.エクセルの活用

実際に計算するととても時間がかかりめんどうなことがわかる。エクセルを使うと簡単に計算できるのでその一例を紹介しよう。

2.1近似直線の出し方

一度自分で計算したものと比べて見ると、理解が深まるかもしれない。